On June 7, 2023, Tanglab, in collaboration with Prof. Yuhai Tu in IBM Watson Research Center, published a research paper titled "Stochastic Gradient Descent Introduces an Effective Landscape-Dependent Regularization Favoring Flat Solutions" in the journal "Physical Review Letters." The paper provides a new perspective on understanding the generalization problem in deep learning and designing new optimization algorithms. The research work is based on the construction of a phenomenological dynamical model and utilizes numerical simulations and analytical calculations to explain the source of the implicit regularization effect of stochastic gradient descent from the perspective of non-equilibrium statistical physics.
Deep learning, as one of the most successful machine learning algorithms in recent years, faces the challenge of generalization, which refers to the performance of a model on unseen data. A typical deep neural network has a large number of model parameters compared to the effective sample size, which is known as overparameterization. Research has shown that contrary to traditional statistical learning theories, deep neural networks in the overparameterized regime are not prone to overfitting but exhibit good generalization performance. In this regime, the landscape of the loss function changes slowly along most directions (flat directions), while it changes rapidly along a few directions (sharp directions), as shown in Figure 1a. This indicates that the landscape of an overparameterized network resembles a highly degenerate valley, where numerous solutions exist with training errors that are almost equally low. However, these solutions differ in their generalization ability, with flatter solutions corresponding to better generalization performance.
On the other hand, stochastic gradient descent (SGD), an optimization algorithm widely used in this field, plays a crucial role in finding flatter solutions with better generalization performance. It updates the parameters by randomly selecting small batches of samples during the iteration process, which can be seen as adding additional noise to the gradient descent. The covariance matrix of this noise is highly correlated with the Hessian matrix, indicating that the dynamical system has a special anisotropic noise: the noise intensity is higher in the sharp directions and lower in the flat directions (Figure 1b). Furthermore, modifying the hyperparameters of stochastic gradient descent, such as the learning rate and batch size, also affects the noise strength, ultimately influencing the generalization ability of the solution. This phenomenon is known as the implicit regularization effect of stochastic gradient descent, and it still lacks a comprehensive theoretical explanation behind it.
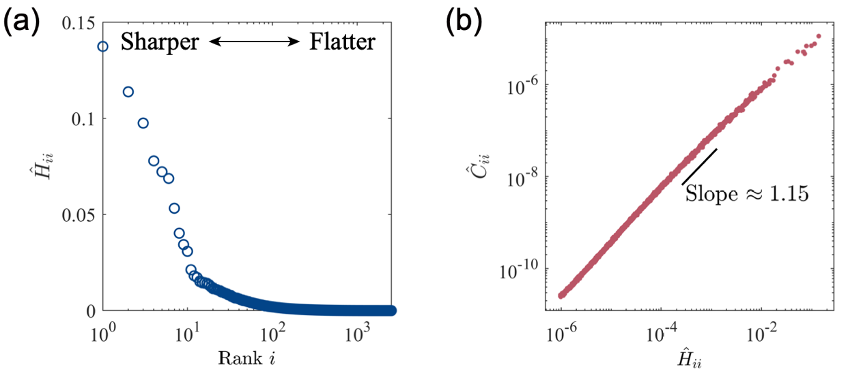
Figure 1: (a) Eigenvalue spectrum of the Hessian matrix corresponding to the loss function of an overparameterized network during training convergence. (b) Alignment relationship between the Hessian matrix and the covariance matrix of noise.
Based on the shape characteristics of overparameterized neural networks, this study constructs an equivalent loss function with high degeneracy in general high-dimensional scenarios. By introducing randomly shifted noise in a manner similar to practical situations, an anisotropic stochastic gradient noise is incorporated. Through numerical simulations of this stochastic dynamical system, the study reveals that the anisotropy of the stochastic gradient descent noise is a necessary condition for the emergence of a preference for flat solutions. Optimization algorithms without noise or with isotropic noise fail to exhibit this preference. Furthermore, this preference is influenced by the hyperparameters of stochastic gradient descent. Increasing the learning rate and noise intensity enhances the tendency for flat solutions, causing the convergence position to move towards flatter solutions. These findings are consistent with previous qualitative results from numerical experiments (Figure 2).
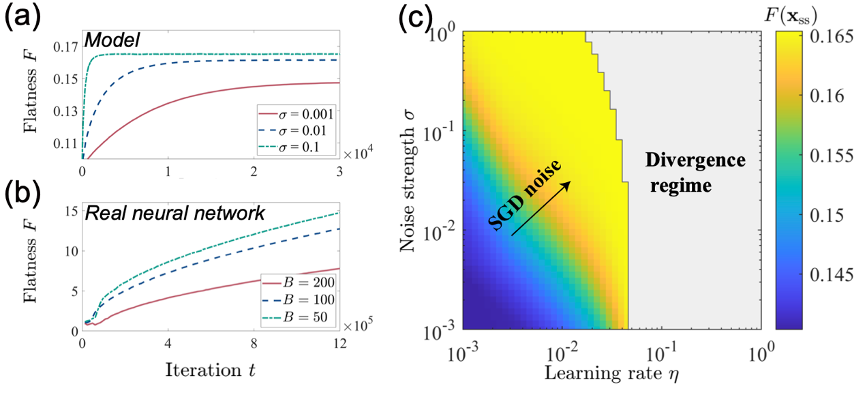
Figure 2: Comparison between model results obtained by varying hyperparameters and the results from real neural networks.
To gain further insight into the aforementioned results, this study continuousizes the iteration equation of stochastic gradient descent and analytically solves the corresponding Fokker-Planck equation. The study reveals that the anisotropy of the stochastic gradient descent noise is equivalent to introducing an additional effective loss function based on the original loss function. This additional loss function decreases with increasing landscape flatness and increases with the hyperparameters of stochastic gradient descent: learning rate and noise strength. This additional loss function term breaks the degeneracy of the original loss function and provides a preference for landscape flatness in the system (Figure 3). From a statistical physics perspective, the anisotropic noise drives the system to a non-equilibrium steady state after stabilization. The resulting macroscopic probability circulation stabilizes the system at flatter solutions, and the strength of this circulation is positively correlated with the hyperparameters. This provides an intuitive physical explanation for the implicit regularization effect.
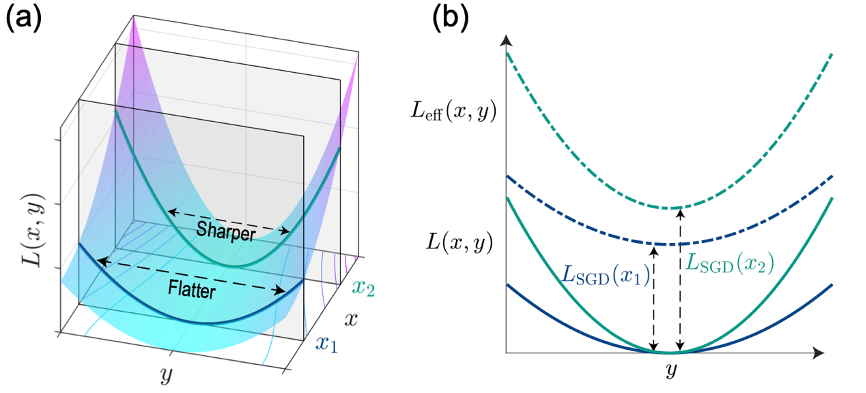
Figure 3: The additional loss function term introduced by SGD breaks the degeneracy of the original loss function.
The first author of this study is Ning Yang, a doctoral student at the Center for Life Sciences, Peking University. Prof. Chao Tang and Prof. Yuhai Tu are the corresponding authors of this study. The research received funding from the National Natural Science Foundation of China. The article can be found at: https://doi.org/10.1103/PhysRevLett.130.237101.