2023年6月7日,北京大学定量生物学中心、物理学院、生命科学联合中心汤超课题组和美国IBM沃森研究中心的涂豫海教授合作,在《Physical Review Letters》杂志上在线发表题为“Stochastic Gradient Descent Introduces an Effective Landscape-Dependent Regularization Favoring Flat Solutions”的研究论文,通过构建唯象的动力学模型,并通过数值模拟和解析计算的方式,从非平衡统计物理的角度解释了随机梯度下降隐式正则化效应的来源,为理解深度学习的泛化问题以及设计新的优化算法提供了新的视角。
深度学习作为近年来最成功的机器学习算法之一,其中核心问题之一是泛化(generalization)问题,即模型在未训练数据上的表现。典型的深度神经网络的模型参数数量远大于有效样本数,这被称为过参数化。研究表明,不同于传统的统计学习理论的预测,深度神经网络在过参数化区间并不容易过拟合,反而具有良好的泛化表现。此时,损失函数景观沿着大多数方向变化缓慢(平坦方向),而在少数方向上变化剧烈(陡峭方向),如图1a所示。这意味着过参数化网络的景观类似高度简并的峡谷,存在大量训练误差几乎一样低的解。然而,这些解对应的泛化能力有所不同,其中更平坦的解对应的泛化性能更好。
另一方面,该领域中广泛应用的优化算法——随机梯度下降(stochastic gradient descent)——对于寻找更为平坦、泛化性能更好的解至关重要。它通过在迭代过程中随机选取小批次样本集来更新参数,可视作在梯度下降上增加了额外噪声。该噪声的协方差矩阵与Hessian矩阵之间存在高度正相关,意味着该动力学系统具有特殊的各向异性噪声:在陡峭方向的噪声强度较大,在平坦方向的噪声强度较小(图1b)。另外,改变随机梯度下降的超参数:学习率和批次大小,也会影响噪声强度,最终影响解的泛化能力。这一现象被称为随机梯度下降的隐式正则化效应,其背后依然缺乏一个完善的理论解释。
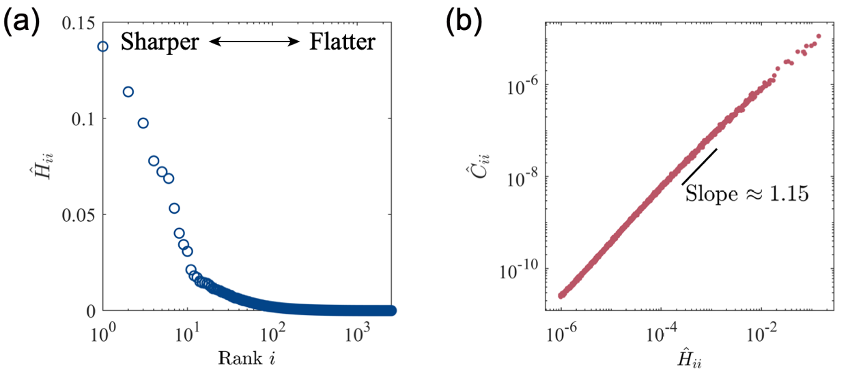
图1 (a)过参数化网络的损失函数在训练收敛时对应的Hessian矩阵的本征值谱 (b)Hessian矩阵与噪声协方差矩阵的正比关系
本研究根据过参数化神经网络的形状特点,构建了一般高维情况下具有高度简并性的等效损失函数,并通过随机偏移的方式引入了与实际情况类似的各向异性的随机梯度噪声。通过对该随机动力学系统进行数值模拟,本研究发现,随机梯度下降噪声的各向异性是产生平坦解倾向性的必要条件,无噪声或各向同性噪声的优化算法均无法产生该倾向性。进一步,该倾向性与随机梯度下降的超参数有关,增加学习率和噪声强度增加了平坦解的倾向性,使得最终收敛解位置朝更平坦的解处移动,这些结果均与前人数值实验定性一致(图2)。
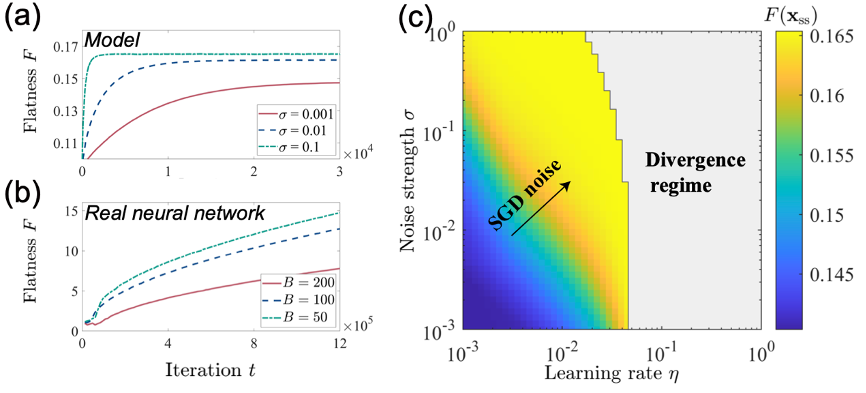
图2 改变超参数的模型结果与真实神经网络结果对比
为了解析理解上述结果,本研究对随机梯度下降的迭代方程连续化并解析求解对应的福克-普朗克方程。本研究发现,随机梯度下降噪声的各向异性相当于在原损失函数基础上引入了一个额外的等效损失函数。该项损失函数随着景观平坦度的增加而减少,并随着随机梯度下降的超参数——学习率和噪声强度而增加。该额外的损失函数项打破了原损失函数的简并性,为该系统提供了关于景观平坦度的倾向性(图3)。从统计物理的角度来看,各向异性噪声使得该系统稳定后处于非平衡稳态,由此产生的宏观的概率环流将该系统稳定在更平坦的解处,而该环流强度与超参数正相关,这便是隐式正则化效应背后的直观物理解释。
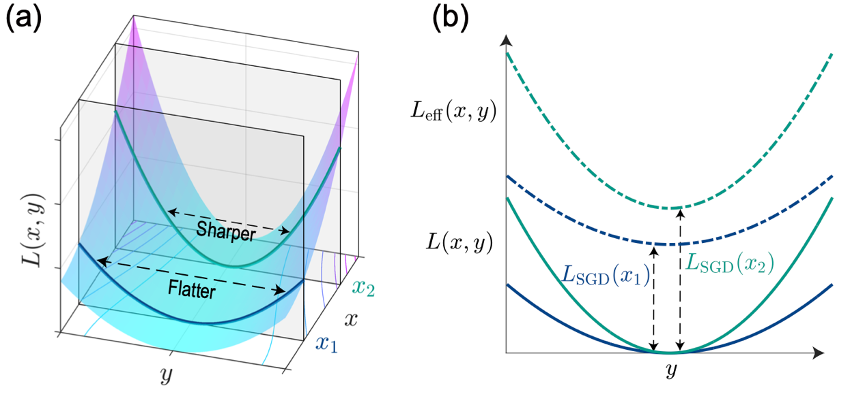
图3 随机梯度下降引入的等效损失函数打破了原有的简并性
本研究的第一作者是北京大学生命科学联合中心博士生杨宁。北大-清华生命科学联合中心PI、北京大学定量生物学中心与物理学院教授汤超和美国IBM沃森研究中心教授涂豫海为本研究的共同通讯作者。该研究得到了国家自然科学基金的资助。文章链接:https://doi.org/10.1103/PhysRevLett.130.237101。